Creative proofs with pigeons and boxes

Mathematics is sometimes like football. Solving a tricky task is not a solitary endeavour, but rather a joint effort requiring creativity and tactics. A lot is going on when secondary school students come together to solve mathematical problems at the ETH Math Youth Academy. A student comes up with an idea, a second one picks it up, suggests a possible solution and passes it to their teammate, who then scores: the problem is solved.

The seven students rack their brains over one problem: on a Saturday night, there is a party in town. How can it be proven that at this party, at which more than two people attend, at least two partygoers have exactly the same number of friends?

The solution can be found in the ‘pigeonhole’ or ‘drawer’ principle, which was first formulated by the German mathematician Peter Gustav Lejeune Dirichlet in 1834:

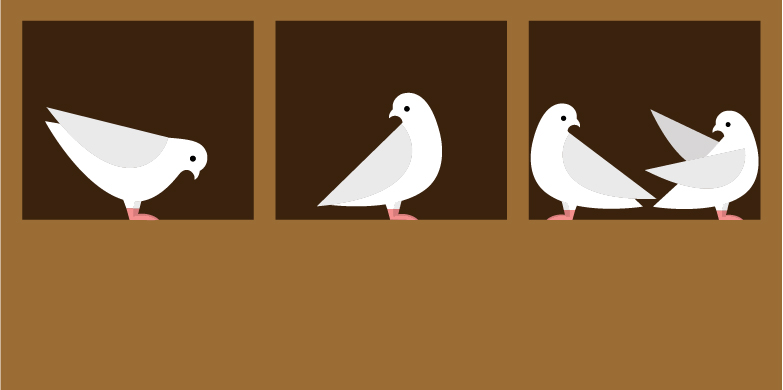
If four pigeons are to be housed in only three pigeonholes, then one pigeonhole must contain at least two pigeons. The same applies if you want to place four pearls in three drawers. The principle can be generalised: when there are more items to be divided up than containers assigned, then at least one container must hold more than one item.

The pigeonhole principle has a wide range of possible applications: as a method of proof, it has proven as useful in geometry as in number theory, combinatorics, graph theory (network theory), formal logic or even theoretical computer science.

The beauty of putative reasons

“That’s the beauty of mathematics: we begin with a simple principle and quickly arrive at surprising conclusions and unexpected results,” says Kaloyan Slavov. The postdoc from the Department of Mathematics researches algebraic geometry and organises the ETH Math Youth Academy. From Bulgaria, Slavov studied at Harvard, Cambridge and MIT.

The ETH Math Youth Academy is part of the educational programme of the National Centre of Competence in Research, The Mathematics of Physics (NCCR SwissMAP). Under the direction of the University of Geneva and ETH Zurich, it promotes research, teaching and knowledge transfer in the fields of mathematics and theoretical physics.

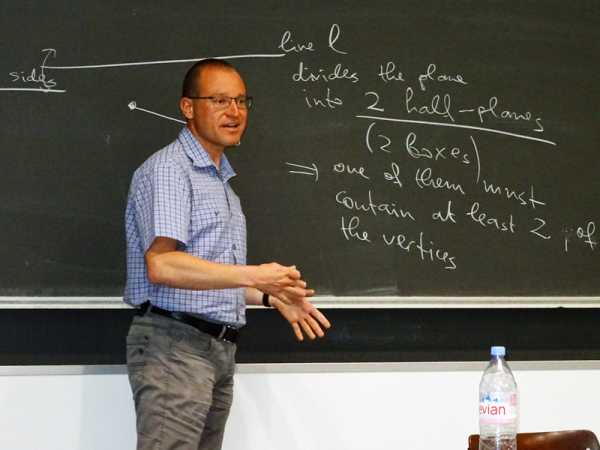
Creative evidence or what is the ‘pigeon’?

The pigeonhole principle quickly becomes challenging, even for secondary school students. They have to apply it to an example from geometry: a straight line intersects a triangle in such a way that it does not touch any of the triangle’s corner points. How can it be proven with the pigeonhole principle that the line cannot intersect all three sides of the triangle?

From this starting point, the students notice that the real difficulty with the principle is to find out on a case-by-case basis which elements should be treated as the ‘pigeons’ and which as the ‘boxes’. This requires a flash of understanding before they can begin to apply the method to a given problem.

This insight is what Slavov wants to impart to the students. By determining what are the pigeons and what are the pigeonholes, they learn to think outside the box and use methods of proof creatively. This ability is useful in university studies, in many areas of mathematics, and even in everyday life.

In the geometry example, the line divides the plane of a triangle into two half-planes. The corner points correspond to the pigeons and the half-planes to the boxes, so that one half-plane contains two corner points and the other half-plane only one. The side of the triangle joining the two corner points that are contained in a single half-plane is not intersected by the line. In the party example, the partygoers correspond to the pigeons and the number of friends to the boxes.

Mathematics is more than calculating numbers

The ETH Math Youth Academy introduces students to mathematical ways of thinking. “The students engage in creative thinking here,” says Slavov. “Creativity is the opposite of routine.” His courses focus on problems that cannot be solved in a routine way, but rather by starting off with a creative idea, arguing in a subtle and logical manner, and applying strict mathematical proofs. The reward, says Slavov, comes from mathematics itself: “People are happy when they recognise the logical order behind things and see that the putative reasons are actually true.”

Fifteen secondary school students take part in the beginners and advanced courses. They enjoy Slavov’s course; they find his lessons exciting and not at all ‘dry’. Here they learn that proofs and mathematics are more than just the calculation of numbers, and are surprised by the multitude of applications, methods and strategies. “The course is cool,” says Yiqi from the Realgymnasium Rämibühl. “There aren’t any traditional solutions here and the path to the solution is creative.” Jonas from Wetzikon also likes the creative side of proofs: “You can’t solve any of the problems here with a template. Instead, you have to find a new solution each time.”