Kreatives Beweisen mit Tauben und Boxen

Manchmal ist Mathematik fast wie Fussball. Das Lösen einer kniffligen Aufgabe ist dann kein einsames Geschäft, sondern ein Gemeinschaftswerk, das Kreativität und Taktik erfordert. Schnell geht es zu und her, wenn Mittelschülerinnen und Mittelschüler zusammenkommen, um an der «ETH Math Youth Academy» mathematische Probleme zu lösen. Ein Schüler wirft eine Idee in die Runde, ein zweiter nimmt den Ball auf, schlägt einen Lösungsweg vor, spielt den Ball der Mitspielerin zu und diese erzielt den Treffer: Die Aufgabe ist gelöst.

Inhaltlich knobeln die sieben Schülerinnen und Schüler an einem Beweis: An einem Samstagabend gibt es eine Party in der Stadt, an der mehr als zwei Personen teilnehmen. Wie lässt sich zeigen, dass mindestens zwei Teilnehmende genau gleich viele Freunde haben?

Die Lösung findet sich in dem so genannten Taubenschlag- oder Schubfachprinzip, das der deutsche Mathematiker Peter Gustav Lejeune Dirichlet 1834 erstmals formulierte. Seinen Namen hat dieses Prinzip, weil man es sich anhand eines Taubenschlags bildhaft vorstellen kann.

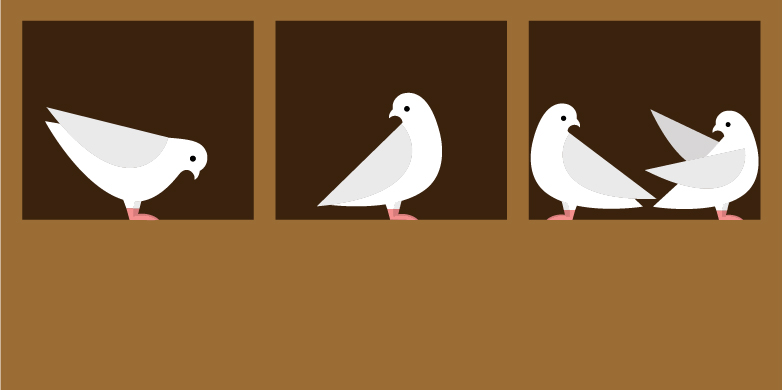
Wenn in einem Taubenschlag, der drei Boxen hat, vier Tauben untergebracht werden, dann müssen in einer Boxe mindestens zwei Tauben sein. Dasselbe gilt, wenn man vier Perlen auf drei Schubfächer verteilt.

Das Prinzip lässt sich verallgemeinern: Jedes Mal, wenn Objekte bestimmten Mengen zugeteilt werden und es dabei mehr Objekte als Mengen gibt, dann muss mindestens eine Menge mehrere Objekte enthalten.

Das Taubenschlagprinzip hat weitreichende Anwendungsmöglichkeiten: Als Beweismethode hat es sich in der Geometrie genauso nützlich erwiesen wie in der Zahlentheorie, der Kombinatorik, der Graphentheorie (Netzwerktheorie), der formalen Logik oder auch in der theoretischen Informatik.

Die Schönheit der vermuteten Gründe

«Das ist die Schönheit der Mathematik: Wir beginnen mit einem einfachen Prinzip und gelangen schnell zu überraschenden Schlussfolgerungen und unerwarteten Resultaten», sagt Kaloyan Slavov. Der Postdoktorand aus dem Departement Mathematik forscht in der algebraischen Geometrie und organisiert die ETH Math Youth Academy.

Die ETH Math Youth Academy gehört zum Ausbildungsprogramm des Nationalen Forschungsschwerpunkts «Mathematik der Physik» (NCCR SwissMAP), das unter der Leitung der Universität Genf und der ETH Zürich Forschung, Lehre und Wissenstransfer im Bereich von Mathematik und theoretischer Physik fördert.

Kreative Beweise oder was ist die «Taube»?

Auch für die Mittelschülerinnen und Mittelschüler wird das Taubenschlagprinzip rasch anspruchsvoller. Sie müssen es auf ein Beispiel aus der Geometrie anwenden: eine Gerade schneidet ein Dreieck, und zwar so, dass sie keinen Eckpunkt des Dreiecks berührt. Wie lässt sich nun mit dem Taubenschlagprinzip beweisen, dass die Gerade nicht alle drei Seiten des Dreiecks schneiden kann?

An dieser Aufgabenstellung bemerken die Schülerinnen und Schüler, dass die eigentliche Schwierigkeit des Taubenschlagprinzips darin besteht, im Einzelfall herauszufinden, welche Elemente sich wie «Tauben» behandeln lassen und welche wie «Boxen». Zuerst braucht es eine zündende Idee, bevor man die Taubenschlagmethode auf ein gegebenes Problem anwenden kann.

Diese Einsicht will Kaloyan Slavov den Schülerinnen und Schülern vermitteln. Indem sie selber festlegen, was sie als Tauben und als Boxen bestimmen, lernen sie, bei der Lösung über den Tellerrand zu schauen und die Beweismethoden kreativ einzusetzen. Diese Fähigkeit nützt im Studium sowie in vielen Gebieten der Mathematik und des Alltags. Selber studierte der Bulgare in Harvard, in Cambridge und am MIT.

Im Geometrie-Beispiel zerteilt die Gerade die Ebene eines Dreiecks in zwei Halbebenen. Dabei entsprechen die Punkte den Tauben und die Halbebenen den Boxen, sodass die eine Halbebene zwei Punkte enthält, die andere aber nur einen. Die Dreiecksseite, die zwei Eckpunkte in einer Halbebene miteinander verbindet, ist dann jene, die von der Geraden nicht zerteilt wird. Im Party-Beispiel entsprechen die Partyteilnehmenden den Tauben und die Anzahl der Freunde den Boxen.

Mathematik ist mehr als Zahlenrechnen

Die ETH Math Youth Academy führt in typische mathematische Herangehensweisen ein. «Die Schülerinnen und Schüler müssen sich nur auf kreatives Denken einlassen», sagt Kaloyan Slavov und ergänzt: «Kreativität ist das Gegenteil von Routine.» Seine Kurse fokussieren auf Probleme, die man nicht mit Routine lösen kann, sondern nur, wenn man von einer kreativen Idee ausgeht, subtil und logisch argumentiert und die Beweise streng mathematisch führt.

Die Belohnung, sagt Slavov, komme aus der Mathematik selbst: «Die Menschen freuen sich, wenn sie die logische Ordnung hinter den Dingen erkennen und sehen, dass die vermuteten Gründe tatsächlich wahr sind.»

15 Schülerinnen und Schüler nehmen an den Kursen für Einsteiger und Fortgeschrittene teil. Kaloyan Slavovs Lektionen gefallen ihnen. Spannend sei der Unterricht, gar nicht «trocken». Hier lerne man, das Beweisen, und dass Mathematik mehr sei als Rechnen mit Zahlen. Überrascht sind sie von der Vielfalt der Anwendungen, Methoden und Lösungsstrategien.

«Der Kurs ist cool», sagt Yiqi aus dem Realgymnasium Rämibühl. «Hier gibt es keine traditionellen Lösungen, und der Weg zur Lösung ist kreativ.» Auch Jonas aus Wetzikon mag die kreative Seite des Beweisens: «Hier kann man kein Problem mit der Schablone lösen, sondern man muss jedes Mal eine neue Lösung finden.»