Mathematik ist überall. Zu Besuch in der Welt von Alessio Figalli
Für seine Forschung über den optimalen Transport hat Alessio Figalli die Fields-Medaille gewonnen. Wer ist dieser Mann? Was zeichnet seine Forschung aus? Warum ist Mathematik ein kreativer Denkprozess? Was haben Wolken, Seifenblasen und Kristalle mit Transportkosten zu tun? Porträt eines Mathematikers, der das Problemlösen zum Beruf gemacht hat.

Mathematik ist überall. Man muss sie nur sehen, sagt Alessio Figalli und blickt zum Himmel. Wolken ziehen über die Stadt Zürich. Einige gross, andere klein. Keine behält ihre Gestalt für lange. Solche Veränderungen der Form interessieren Alessio Figalli. Sie bieten ihm die Anschauung, um die Mathematik dahinter zu verstehen. Die Mathematik, für die Figalli die Fields-Medaille erhalten hat: die höchste Auszeichnung für einen Mathematiker unter 40 Jahren.
Mathematik ist überall. Sie zu erkennen, erfordert Kreativität, sagt Figalli auf dem Weg zum ETH-Hauptgebäude, wo er sein Büro hat. Figalli ist zu Fuss unterwegs. Das ist eine gute Art, um neue Ideen für eine mathematische Fragestellung auszudenken. Zumal dann, wenn es sich um ein Problem handelt, über das sich die Mathematiker seit Jahren – oder noch länger – den Kopf zerbrechen. «Um der erste zu sein, der eine offene Frage lösen kann, muss man eigene Ideen entwickeln. Dann versucht man die Ergebnisse aus verschiedenen Bereichen miteinander zu verknüpfen und neue Techniken zur Lösung des Problems zu entwerfen. Das ist ein kreativer Denkvorgang», sagt Figalli.
Das Geheimnis der Wolken
Mit Blick auf die Wolken ist das geglückt: Zusammen mit anderen Mathematikern konnte Figalli beweisen, dass sich gewisse Veränderungen der Form von Wolken mathematisch wie ein «optimaler Transport» berechnen lassen. Es sind daher dieselben – oder verwandte – Gleichungen auf Wolken anwendbar wie man sie zur Berechnung eines möglichst günstigen Transportwegs von Ressourcen oder Personen verwendet.
Die Lösungsidee war: Wenn eine Wolke abrupt ihre Gestalt ändert, bewegen sich unzählige Wolkenteilchen aus ihrer Position in eine andere. Man kann sich diese Bewegung auch so vorstellen als würden die Partikel von einem Ort zu einem anderen transportiert. Das trifft namentlich auf die Wolkenformationen einer Grosswetterfront zu. Diese verändern sich oft so sprunghaft und plötzlich, dass es sehr anspruchsvoll ist, sie mathematisch zu beschreiben.
Als Figalli 2005 an dieses «semigeostrophische Problem» herantrat, war der Zusammenhang zwischen Transportoptimierung und Meteorologie seit den 1990er-Jahren bekannt. Im Detail fehlten aber wichtige Resultate. So machte er sich daran, die sehr komplexen Differentialgleichungen und ihre Eigenschaften und Abhängigkeiten zu untersuchen.
Differentialgleichungen beschreiben Bewegungen und Veränderungen. Sie sind eines der wichtigsten Werkzeuge der Natur- und Ingenieurwissenschaften und eine Voraussetzung für viele technische Errungenschaften der modernen Gesellschaft. Eine bekannte Differenzialgleichung ist die Monge-Ampère-Gleichung.
Im Kern beschreibt sie, welcher Weg am effizientesten ist, um Objekte und Ressourcen zu transportieren. Gaspard Monge (1746-1818) war ein französischer Mathematiker und Minister unter Napoleon. Er wollte wissen, wie sich das benötigte Baumaterial möglichst kostengünstig zu den Baustellen für Befestigungsanlagen transportieren liess. Oder umgekehrt gefragt: Zu welchem Standort bringt man das Baumaterial am besten, wenn man die Transportkosten minimieren will?
Die Kosten der Veränderung
Auf die Wolken übertragen heisst das: Wenn man weiss, dass die Partikel auf dem Weg von der Anfangsverteilung zur Endverteilung die «Transportkosten» minimieren, kann man ihren optimalen Weg berechnen. Auf diese Weise erhält man Information, wie die Wolken ihre Form verändern. Sieben Jahre lang untersuchten Figalli und seine Weggefährten die Monge-Ampère-Gleichung.
2012 kam der Durchbruch: sie konnten für diese Gleichung grundlegende Resultate über die Eigenschaften von Lösungen beweisen. Ausserdem zeigten sie, dass sich die Gleichung eignet, um die Veränderung von Wolkenformationen zu beschreiben.
«Bei der Anwendung der Theorie des optimalen Transports auf physikalische und chemische Beispiele, spielt es eine wichtige Rolle, dass sich der Begriff der minimalen ‹Kosten› in vielen Fällen auf die Energie bezieht», erklärt Figalli, «denn die Natur minimiert Energie.»
Neben den Wolken hat Figalli auch Formveränderungen von Seifenblasen und Kristallen untersucht. Sowohl Seifenblasen als auch Kristalle streben nach einer Form, die ihre Oberflächenenergie möglichst geringhält. Physikalisch handelt es sich zwar um verschiedene Arten von Energie, mathematisch jedoch sind die Gleichungen sehr ähnlich. Man kann die Theorie des optimalen Transports auf beide anwenden, um zu beschreiben, wie sich ihre Form verändert, wenn man Energie zuführt. Danach lässt sich untersuchten, wie die Partikel von der Konfiguration mit minimaler Energie zu derjenigen mit erhöhter Energie transportiert werden.
Origineller Denker und Problemlöser
Es gibt Mathematiker, die entwickeln eine neue Technik, mit der sie sozusagen die Tür aufstossen zu einem völlig neuen Forschungsgebiet: Das war so, als Isaac Newton (1642-1726) und Gottfried Wilhelm Leibniz (1646-1716) die Differentialrechnung einführten. Alessio Figalli ist ein anderer Typ Mathematiker. Er entwirft keine neuen Theorien und Modelle, sondern konzentriert sich darauf, Lösungen für bestehende Probleme zu entwickeln. Nicht irgendwelche, sondern mit Vorzug solche, an denen Mathematiker schon lange herumstudieren.
Wer in diesem Wettbewerb als erster ein Problem lösen und durch einen strengen Beweis begründen will, braucht neben profundem Wissen viel Kreativität und Originalität. Dazu gehört, dass man enttäuschte Erwartungen wegsteckt: «Von der Idee bis zum strengen Beweis ist es ein weiter Weg. Oft bin ich gescheitert, immer habe ich dazu gelernt», sagt Figalli. Er hatte das Glück, dass seine Lehrer zu den originellsten und ideenreichsten Mathematikern gehören: Luigi Ambrosio in Pisa, Cédric Villani in Lyon, Fields-Medaillenträger von 2010, und Luis Angel Caffarelli in Austin.
In Austin, wo Figalli sieben Jahre Professor war, bevor er an die ETH kam, nannten sie ihn ein «Ass unter den Problemlösern». Figalli ist ein sportlicher Mann: Er bevorzugt Basketball und Fussball. Er ist verheiratet und bezeichnet sich selbst als einen zuverlässigen und effizienten Forscher. Mathematik, sagt er, entsteht im Dialog. An Zürich schätzt er die hervorragenden Studierenden, das lebendige und dynamische Umfeld an der ETH Zürich, und dass es an der Universität Zürich ebenfalls ein starkes Institut für Mathematik gibt.
Blitzkarriere nach später Eingebung
Seine Karriere verlief schnell: Nach dem Studium an der Scuola Normale Superiore in Pisa, einer Talentschmiede, die nur wenige, besonders originelle Studierende aufnimmt, schloss er sein Doktorat in nur einem Jahr ab. Als er abschloss, wurde er sogleich Assistenzprofessor in Nizza. Mit 25 wurde er zum ausserordentlichen Professor an der Universität von Texas in Austin ernannt, mit 27 zum ordentlichen Professor befördert und mit 32 an die ETH Zürich berufen.
Figalli fühlte sich nicht früh zur Mathematik berufen: Seine Leidenschaft für die Mathematik wurde erst geweckt, als ihn ein Lehrer im Gymnasium überzeugte, an der Mathematik-Olympiade teilzunehmen. Sein Vater war Ingenieur-Professor, und als Kind dachte er, Mathematik sei ein Werkzeug für Ingenieure. Dass sie ein eigenes Berufsfeld sein könnte, war ihm nicht bewusst. Heute ist es sein Anliegen, «dass die Jungen wissen, dass Mathematik ein kreativer Beruf ist.»
Mathematik ist überall.

Literaturhinweise
Figalli A, Guionnet A: Universality in several-matrix models via approximate transport maps. Acta Math. 217 (2016), no. 1, 81-176.
De Philippis G, Figalli A: Partial regularity for optimal transport maps. Publ. Math. Inst. Hautes Études Sci. 121 (2015), 81-112.
De Philippis G, Figalli A: W^{2,1} regularity for solutions of the Monge-Ampère equation. Invent. Math. 192 (2013), no. 1, 55-69.
Ambrosio L, Colombo M, De Philippis G, Figalli A: Existence of Eulerian solutions to the semigeostrophic equations in physical space: the 2-dimensional periodic case. Comm. Partial Differential Equations 37 (2012), no. 12, 2209–2227.
Figalli A, Maggi F, Pratelli A: A mass transportation approach to quantitative isoperimetric inequalities. Invent. Math. 182 (2010), no. 1, 167-211.
Hintergrundinformationen für Medien

Text-, Video- und Fotomaterial inklusive Video-Statements von Fields-Medaillenträger Alessio Figalli und ETH-Präsident Lino Guzzella gibt es unter www.ethz.ch/fields-medaille-fuer-figalli .

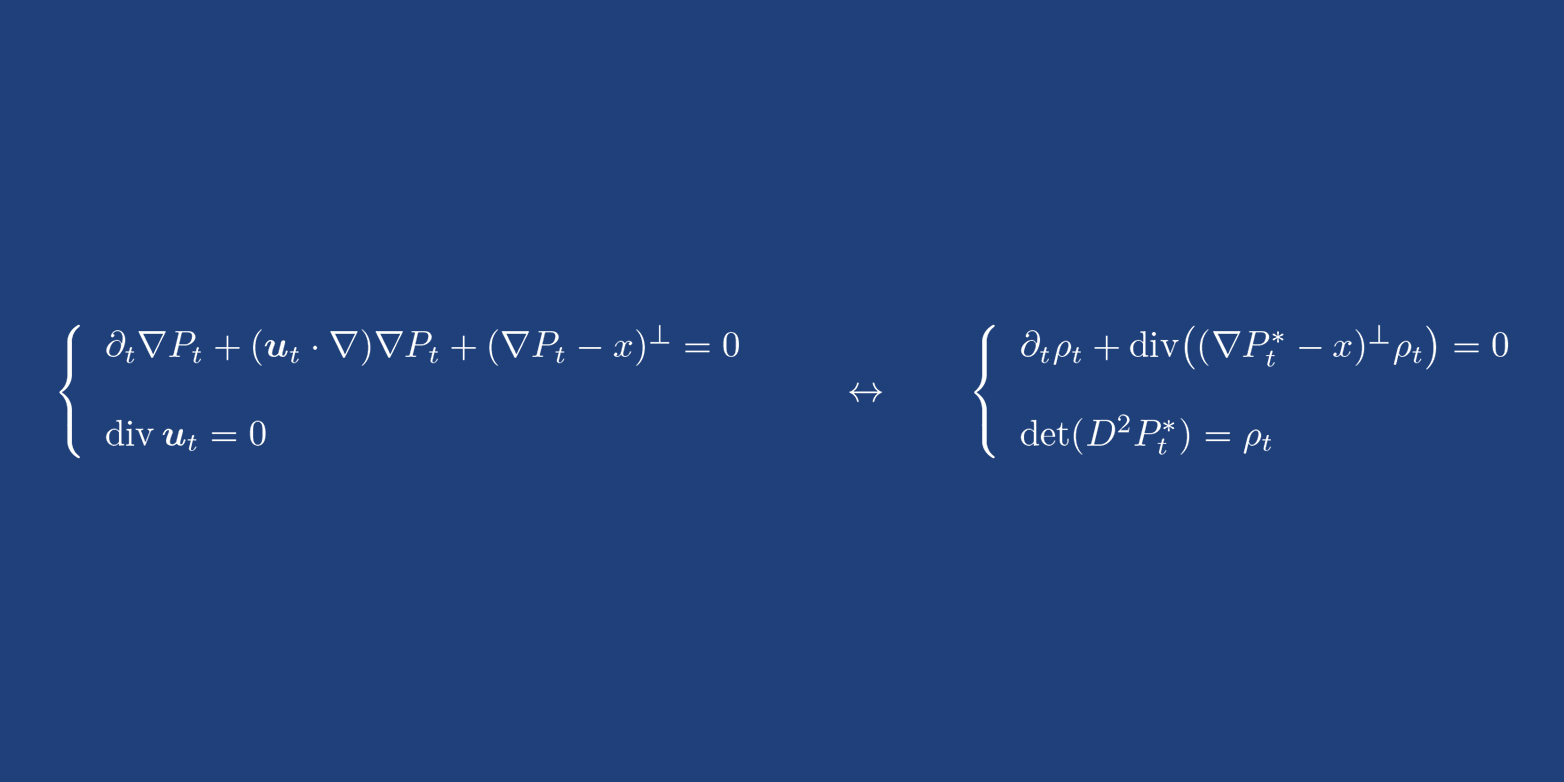

Kommentare
Noch keine Kommentare