Turbulente Angelegenheiten: Wie Forschende Schockwellen besser simulieren

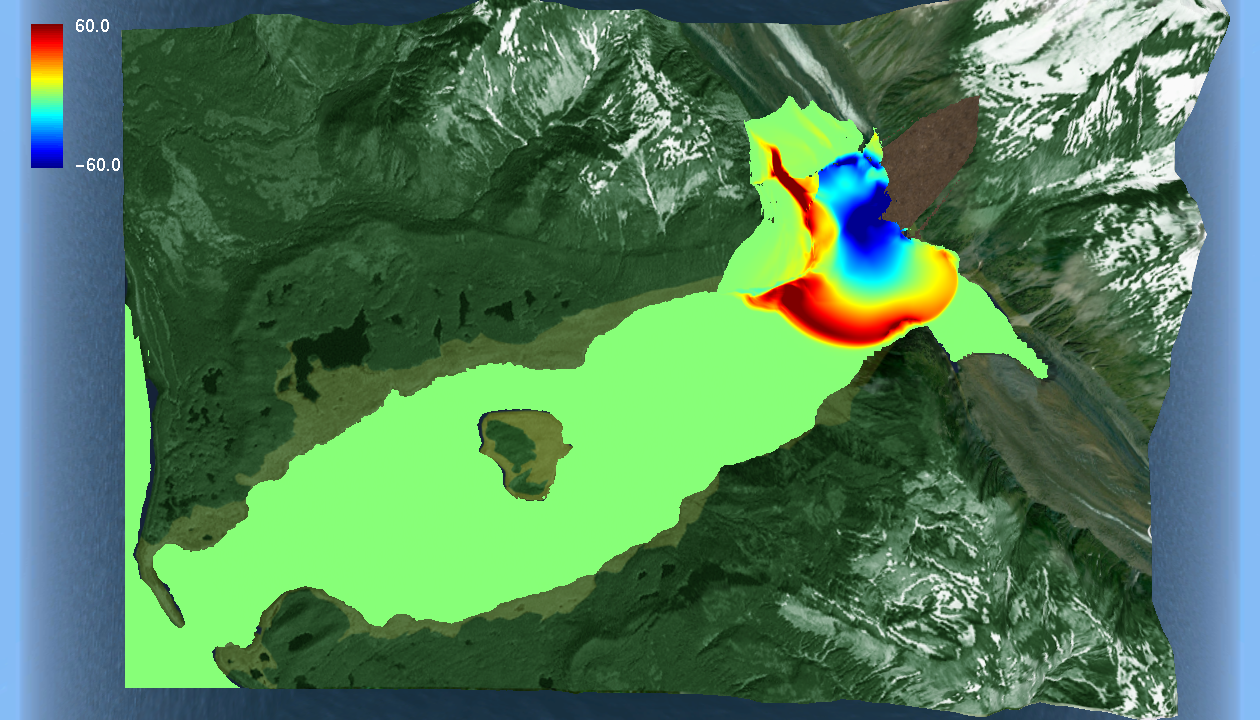
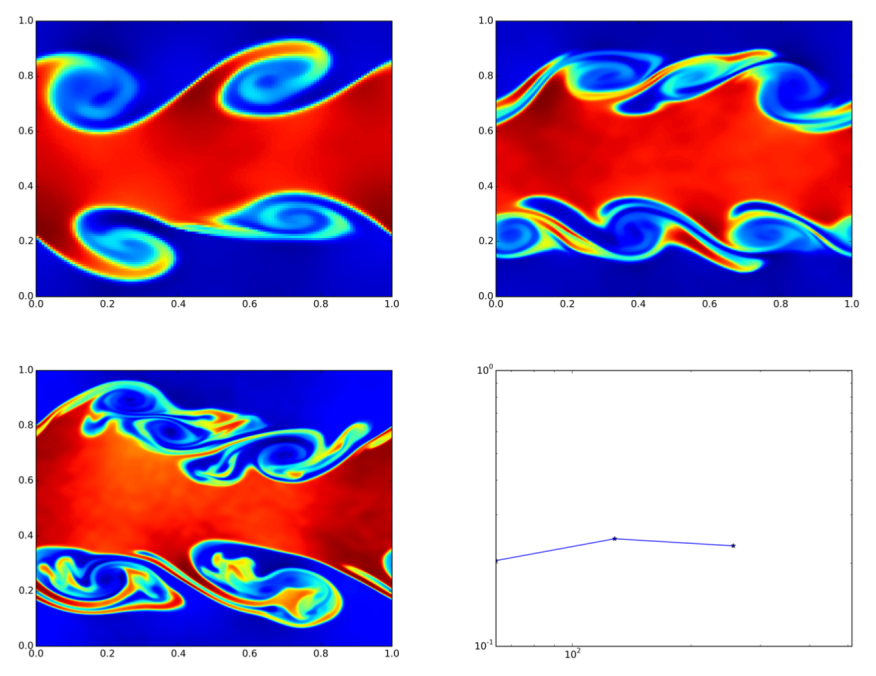
Dennoch: Streng genommen sind diese Methoden nicht mathematisch präzis. Und: Für einige Phänomene sind sie an ihre Grenzen gestossen. «Normalerweise würde man erwarten, dass eine höhere Auflösung genauere Ergebnisse liefert», sagt Mishra. Anders gesagt: Bezieht man in eine Berechnung mehr einzelne Punkte aus Zeit und Raum ein, sollte der Fehler eigentlich kleiner werden und die berechneten Näherungswerte sollten die Realität besser abbilden. Doch bei stark turbulenten Flüssigkeiten funktioniert das nicht, wie Mishra zeigte. Im Gegenteil: Bei hoher Auflösung erzielte Ergebnisse stimmen dann überhaupt nicht mit den Ergebnissen von schwächer aufgelösten Berechnungen überein – sie konvergieren nicht, wie der Mathematiker sagt, sondern sehen komplett anders aus. «Das bedeutet auch, dass sich für solche Phänomene keine Vorhersagen berechnen lassen.»

Äusserst nützlich: zufällige Störungen

Darum haben Mishra und sein Team nach einer Möglichkeit gesucht, diese Schwierigkeiten beim Simulieren stark turbulenter Ströme zu überwinden, und zwar mit sogenannten statistischen Lösungen. Dazu haben die Forschenden das Problem «randomisiert», also den Zufall berücksichtigt: Sie erzeugten in den untersuchten Strömungen viele winzige, zufällige Störungen – und analysierten dann das gemittelte Ergebnis. «Das ist die Grundlage für statistische Lösungen», erklärt Mishra. «Wenn sich einzelne Messungen oder Experimente nicht konvergent verhalten, kann man sich stattdessen Durchschnittswerte anschauen.» Einfach ausgedrückt: «Bei turbulenten Strömungen sind die Details das Problem. Deshalb sieht man mit Durchschnittswerten mehr Struktur.»

Damit nicht genug: Zusätzlich müsse man auch berücksichtigen, dass die statistischen Eigenschaften von Strömungen an verschiedenen Orten im Raum voneinander abhängig seien, wie Mishra erklärt. Zum Beispiel beim Wetter: Die Temperatur in Zürich wirkt sich nicht nur auf nahe gelegene, sondern auch auf weit entfernte Orte aus, etwa auf die Temperatur in München. «Darum müssen wir anstelle einzelner Punkte die Korrelationen zwischen den Punkten untersuchen», sagt Mishra.

Lösung für turbulente und explosive Probleme

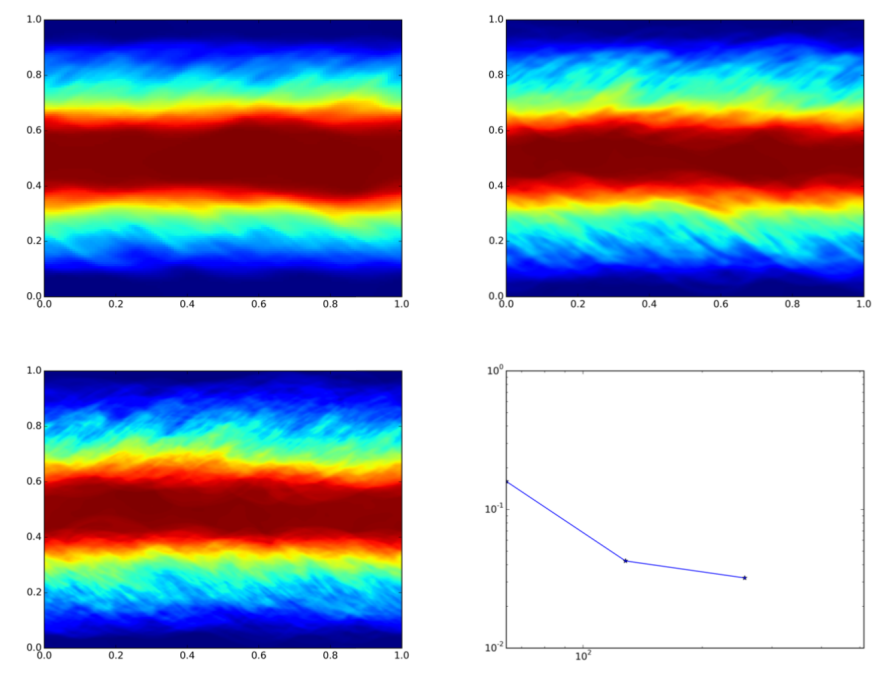
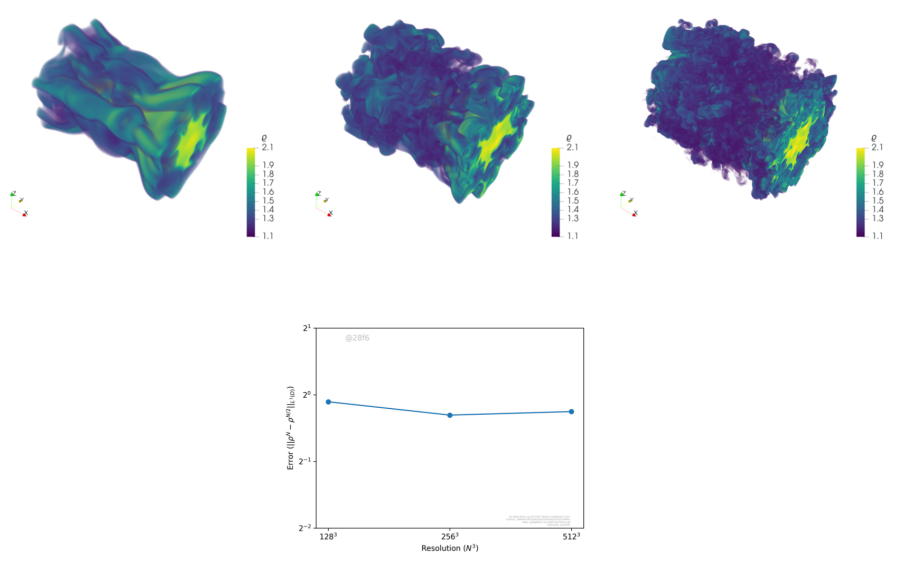
Soweit die Theorie. Wie sieht das nun in der Praxis aus? «Wir können solche statistischen Lösungen berechnen», sagt Mishra. Tatsächlich konvergierten die berechneten Mittelwerte nun mit höherer Auflösung, wie das Team erkannte. Und: Das galt nicht nur für spezifische Grössen, etwa die Dichte oder die Geschwindigkeit einer Strömung, sondern auch für die statistischen Abweichungen dieser Grössen und ihre Wahrscheinlichkeitsverteilung. «Bislang hat jede unserer Testsimulationen mit vereinfachten, zweidimensionalen Strömungen funktioniert.» Ob Mittelwerte, Abweichungen, Wahrscheinlichkeitsverteilung, Korrelationen –alle statistischen Werte konvergieren, und die erhaltenen Lösungen sind stabil.

Nach diesen ersten 2-D-Simulationen führte Mishras Team mithilfe des Supercomputers «Piz Daint» am CSCS in Lugano Simulationen in 3-D durch. Jüngst haben die Forschenden ihren Code optimiert, sodass sie die Simulationen auf «Piz Daint» um mehr als das Zehnfache beschleunigen konnten.

In den Simulationen wurden auf die Strömungen zunächst virtuell bestimmte Scherkräfte ausgeübt, um die Entstehung von sogenannten Kelvin-Helmholz-Instabilitäten zu simulieren. Diese führen zu spezifischen Wirbeln, wie sie beispielsweise im kräuselnden Rauch einer Kerze sichtbar sind, ebenso in bestimmten Wolkenformationen oder in Gasen in der Atmosphäre von Planeten. Auch hier zeigten die Ergebnisse: Betrachten die Forschenden einzelne Simulationen, ist keine Konvergenz zu erkennen. «Arbeiten wir aber mit den statistischen Eigenschaften zahlreicher Simulationen, wie Mittelwerte, Abweichungen und Wahrscheinlichkeiten, konvergieren die Lösungen», bestätigt Mishra.

Von der Hypothese zum mathematischen Theorem

Kürzlich führte sein Team auf «Piz Daint» ähnliche Simulationen eines anderen Phänomens durch, die sogenannte Richtmeyer-Meshkov-Instabilität. Diese kennt man vor allem in der Astrophysik, sie entsteht, wenn eine Schockwelle auf die Grenzfläche zwischen zwei verschiedenen Strömungen trifft. «Eine solche Instabilität ist heftig, ähnlich wie eine Explosion», erklärt Mishra. Wiederum zeigten die Simulationen und Analysen des Teams, dass die statistischen Lösungen vieler Simulationen mit zunehmender Auflösung konvergieren, wohingegen man mit einzelnen Simulationen ohne Konvergenz nicht weit kommt.

«Durch die Computersimulationen verstehen wir nun viel besser, was vor sich geht», fasst Mishra zusammen. «Wir konnten unsere Hypothese über den Nutzen statistischer Lösungen überprüfen und dabei eine gewisse Intuition für diese Lösungen entwickeln. Aber jetzt müssen wir Papier und Bleistift in die Hand nehmen, um die Mathematik unserer Hypothese rigoros zu beweisen, also ein Theorem aufzustellen, das auf den grundlegenden Axiomen der Mathematik basiert.» Für einen Mathematiker wie Mishra ist dies unerlässlich – eine Art letzte, übergeordnete Ebene der Wahrheit.