Ein unendlicher Spass an der unendlichen Vielfalt

Zu den erstaunlichsten Erkenntnissen der Mathematik gehört die Entdeckung, dass es verschiedene Arten von Unendlichkeiten gibt – und es war lange ein offenes Problem, ob gewisse dieser Unendlichkeiten widerspruchsfrei verschieden gross sein können.

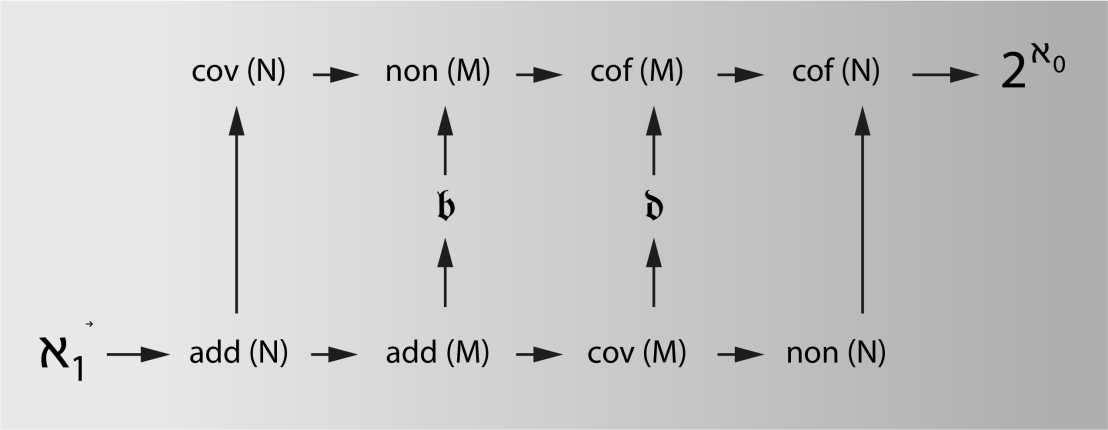
Ein mathematischer Logiker, der sich seit Jahren intensiv damit auseinandersetzt, ist Saharon Shelah von der Hebräischen Universität Jerusalem. Als Gastredner der diesjährigen Paul Bernays Lectures wird er über aktuelle Entwicklungen im «Ringen um die Grösse des Unendlichen» berichten. Shelah ist ein ausgewiesener Kenner der mathematischen Unendlichkeitsproblematik. Vor einem Jahr gelang ihm – mit Martin Goldstern und Jakob Kellner von der externe Seite TU Wien – der Beweis, dass zehn – und nicht mehr – Unendlichkeiten verschieden gross sein können, und dass man sie ihrer Grösse nach im so genannten Cichoń-Diagramm (siehe Abbildung unten) anordnen kann.

Das war ein bahnbrechender Beweis wie die Geschichte zeigt: Die moderne, mathematische Debatte um die Unendlichkeit begann mit einer Reihe von Entdeckungen, die der deutsche Mathematiker Georg Cantor (1845-1918) in den 1870er-Jahren machte. Mit der – von ihm begründeten – Mengenlehre stellte er fest, dass man in der Mathematik viele, ja unendlich viele Unendlichkeiten unterscheiden kann. Cantor begriff die Unendlichkeit nämlich als eine Menge, die eine unendliche Anzahl von Elementen (oder Zahlen) enthält. Indem er sich an der unendlichen Menge der natürlichen Zahlen orientierte – das sind diejenigen Zahlen, die man im Alltag beim Zählen verwendet, also 1, 2, 3, 4, 5 usw. –, konnte er zeigen, dass es zwei grundsätzlich verschiedene Arten von Unendlichkeit gibt.

Nämlich die «abzählbar unendlichen» Mengen, die gleich viele Elemente (oder Zahlen) haben wie die unendliche Menge der natürlichen Zahlen, und die «überabzählbar unendlichen» Mengen, die mehr Elemente enthalten.  Zu der zweiten Art gehört die unendliche Menge der reellen Zahlen. Sie enthält neben ganzen Zahlen, auch negative Zahlen, Brüche, Wurzeln oder mathematische Konstanten wie π etc. Mathematiker nennen die unendliche Menge der reellen Zahlen das «Kontinuum».

Wie Cantor bewies, ist das Kontinuum tatsächlich grösser als die abzählbar unendliche Menge der natürlichen Zahlen. Diese ist ihrerseits die kleinste unendliche Menge. Er untersuchte auch, ob es zwischen den unendlichen Mengen der natürlichen und der reellen Zahlen noch eine – oder sogar mehrere –andere Arten von unendlichen Mengen geben kann. Er vermutete, dass dies nicht der Fall sei, und diese Vermutung nennt man die Kontinuumshypothese.

Aus der Vielfalt heraus das Unendliche eingrenzen

Zu seinem Leidwesen konnte er das nie beweisen – bis heute ist dieser Beweis niemandem gelungen. Im Gegenteil: Nach dem Zweiten Weltkrieg bewiesen die Logiker Kurt Gödel (1906–1978) und Paul Cohen (1934-​2007), dass man die Kontinuumshypothese innerhalb der bekannten axiomatischen Mengenlehre weder beweisen noch widerlegen kann. Man darf sowohl annehmen, zwischen der Menge der natürlichen Zahlen und dem Kontinuum gebe es noch weitere Arten von Unendlichkeit, als auch, dass es da keine gebe. Weder die eine noch die andere Aussage widerspricht den Grundsätzen dieser Mengenlehre.

Wie alle mathematischen Theorien baut die genannte Mengenlehre auf Axiomen auf. Das sind als wahr akzeptierte Grundsätze, aus denen die weiteren mathematischen Aussagen widerspruchfrei herzuleiten sind. Als Standardsystem der Mengenlehre – und damit als Grundlage der Mathematik insgesamt – hat sich das Axiomensystem ZFC etabliert, das auf Ernst Zermelo (1871–1953) und Abraham Fraenkel (1891–1965) zurückgeht. Es umfasst neun Axiome, darunter das Unendlichkeitsaxiom, dank dem man über unendliche Mengen auch Aussagen machen kann.

Die Kontinuumshypothese und die Frage, wie viele Arten von Unendlichkeit sich finden lassen, beschäftigt die Mathematik bis heute, wobei sich die Ansätze je nach philosophischer Haltung unterscheiden: So versuchen Mengentheoretiker wie Hugh Woodin, der Gastredner der Bernays Lectures 2016, die Kontinuumshypothese doch noch zu widerlegen oder zu beweisen, indem sie die ZFC-​Axiome mit neuen erweitern. Woodin folgt dabei seiner Überzeugung, dass es nur ein «richtiges» Modell der Mengelenlehre geben kann.  

Einen anderen, etwas «verspielteren» Ansatz verfolgt Saharon Shelah, von dem man erzählt, er liebe es, anspruchsvolle Probleme zu lösen, und der von sich selbst sagt, seine mathematikphilosophische Position sei der Hedonismus: «Mathematik macht Spass!» Shelah fragt sich weniger, ob die Kontinuumshypothese unlösbar sei, sondern er sagt sich umgekehrt, wenn sie so oder so keine Widersprüche zu den Axiomen der Mathematik auslöst, dann ist man frei  davon auszugehen, dass sie nicht gilt, und anschliessend zu untersuchen, ob es zusätzliche Arten von  Unendlichkeit gibt. Im Prinzip könnte es zwischen der abzählbaren Unendlichkeit und dem Kontinuum unendlich viele Unendlichkeiten geben.

Einige lassen sich ausschliessen: «Für unendliche Mengen ist jede erdenkliche Grösse möglich, die keinen Widerspruch zu den ZFC-Axiomen auslöst», sagt Lorenz Halbeisen, Privatdozent und Logiker der ETH Zürich, der mit Shelah geforscht hat. Dafür hat Shelah die so genannte Proper Forcing-Technik entwickelt. Mit dieser Methode lässt sich die ZFC-Mengenlehre um neue unendliche Mengen erweitern, und man kann sehr verschiedene Modelle von ZFC konstruieren, um damit gewisse Aussagen zu überprüfen. «Mit dieser Technik kann man sehr gut angeben, was in einem Modell jeweils möglich ist und welche Grössen man für unendliche Mengen ausschliessen kann», sagt Halbeisen.

Ein Gespür für erstaunliche Zusammenhänge