Erste Schritte auf dem Weg zum zuverlässigen Quanten-Maschinenlernen

Wer Pilze sammelt, weiss, dass es besser ist, die giftigen und die ungiftigen auseinanderzuhalten. Nicht auszudenken, was passierte, wenn jemand die giftigen verspeiste. Bei solchen «Klassifikationsproblemen», bei denen es darum geht, bestimmte Objekte voneinander abzugrenzen und die gesuchten anhand von Merkmalen bestimmten Klassen zuzuordnen, können Computer schon heute die Menschen sinnvoll unterstützen. Intelligente Verfahren des maschinellen Lernens können Muster oder Objekte erkennen und automatisch aus Datensätzen heraussuchen – zum Beispiel könnten sie aus einer Fotodatenbank diejenigen heraussuchen, die ungiftige Pilze zeigen.

Besonders bei sehr grossen und komplexen Datensätzen kann maschinelles Lernen wertvolle Ergebnisse liefern, die Menschen nicht oder nur mit sehr viel mehr Zeitaufwand herausfänden. Bei gewissen Rechenaufgaben stossen jedoch auch die schnellsten heute verfügbaren Computer an ihre Grenze. Hier kommt das grosse Versprechen der Quantencomputer ins Spiel, dass sie dereinst auch solche Berechnungen superschnell ausführen werden, die klassische Computer nicht in nützlicher Frist lösen können. Der Grund dieser «Quantenüberlegenheit» liegt in der Physik: Quantencomputer rechnen und verarbeiten Information, indem sie gewisse Zustände und Wechselwirkungen ausnutzen, die innerhalb von Atomen oder Molekülen oder zwischen Elementarteilchen vorkommen.

Die Tatsache, dass sich Quantenzustände überlagern und verschränken können, schafft eine Grundlage, dank derer Quantencomputer Zugang zu einer grundlegend reichhaltigeren Verarbeitungslogik haben. Zum Beispiel rechnen Quantencomputer – anders als klassische Computer – nicht mit Binärcodes oder Bits, die Information nur als 0 oder 1 verarbeiten, sondern mit Quantenbits oder Qubits, die den Quantenzuständen von Teilchen entsprechen. Der entscheidende Unterschied ist, dass Qubits pro Rechenschritt nicht bloss einen Zustand – 0 oder 1 – realisieren können, sondern zusätzlich auch einen Zustand, in dem sich beide überlagern. Diese allgemeinere Art der Informationsverarbeitung ermöglicht wiederum eine drastische Beschleunigung der Berechnungen bei bestimmten Problemen.

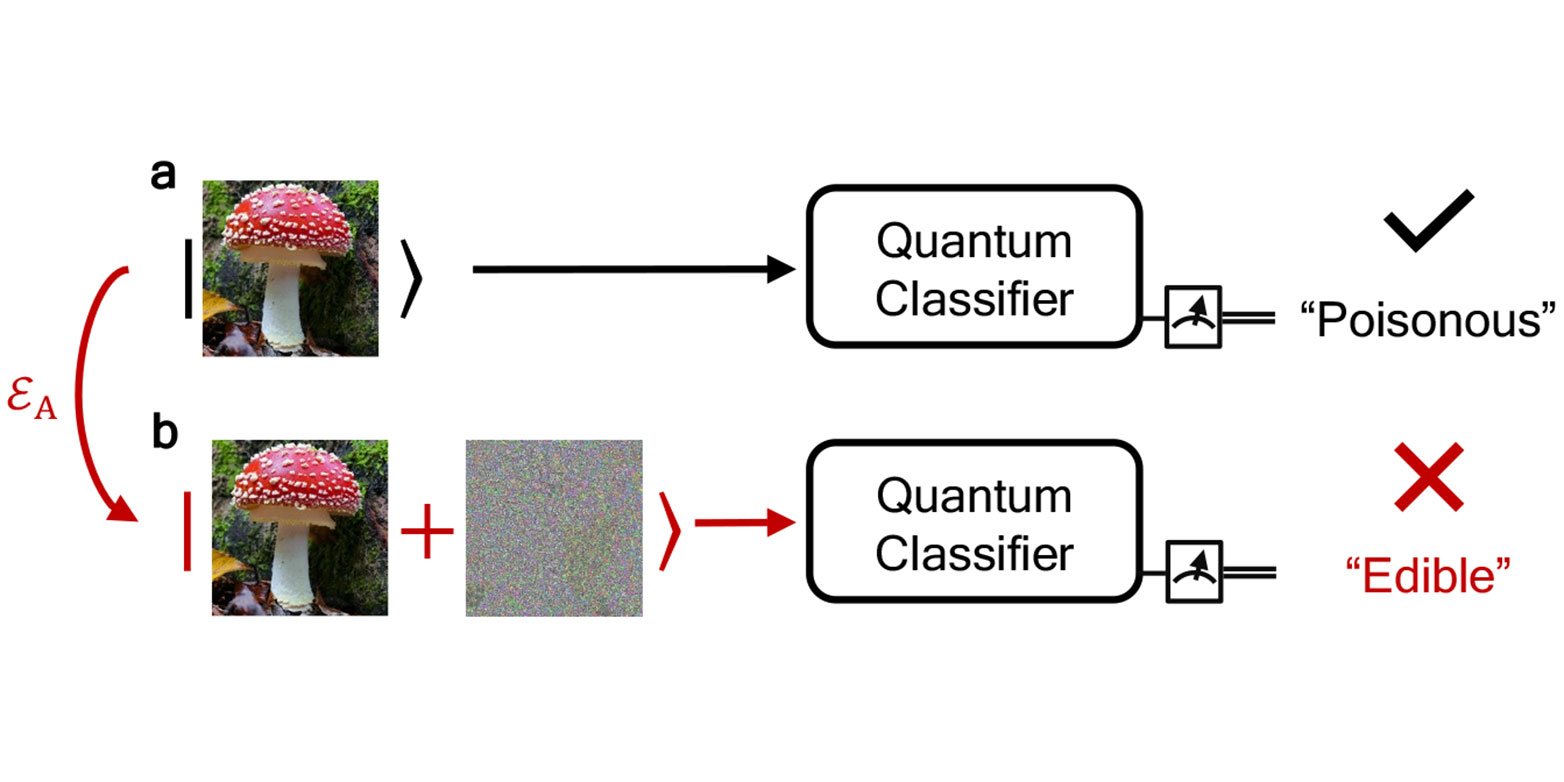
Klassisches Wissen in die Quantenwelt übersetzen

Diese Geschwindigkeitsvorteile des Quantenrechnens sind auch eine Chance für Anwendungen des maschinellen Lernens – schliesslich könnten die Quantencomputer die riesigen Datenmengen, die maschinelle Lernverfahren benötigen, damit sie die Genauigkeit ihrer Ergebnisse verbessern, viel schneller berechnen als klassische Computer.

Um das Potenzial des Quantenrechnens wirklich auszunutzen, muss man die klassischen Verfahren des maschinellen Lernens jedoch auf die Eigenheiten der Quantencomputer anpassen. Zum Beispiel muss man die Algorithmen, also die mathematischen Berechnungsregeln, die beschreiben, wie ein klassischer Computer ein bestimmtes Problem löst, für Quantencomputer anders formulieren. Gut funktionierende «Quantenalgorithmen» für maschinelles Lernen zu entwickeln, ist dabei nicht ganz trivial, denn auf dem Weg dahin, sind noch einige Hürden zu überwinden.

Das hat zum einen mit der «Quanten-Hardware» zu tun. An der ETH Zürich verfügen Forschende derzeit über Quantenrechner, die mit bis zu 17 Qubits arbeiten. Sollten Quantencomputer dereinst ihr volles Potenzial ausspielen, könnten jedoch tausende bis hunderttausende Qubits erforderlich sein.

Quantenrauschen – oder die Unvermeidlichkeit der Fehler

Eine Herausforderung, die sich bei Quantencomputern stellt, betrifft deren Fehleranfälligkeit. Die heutigen Quantencomputer funktionieren mit einem sehr starken «Rauschen» (engl. noise), wie Fehler oder Störeinflüsse in der Fachsprache heissen. Für die Amerikanische Physikalische Gesellschaft stellt dieses Rauschen «das grösste Hindernis zur Vergrösserung und Leistungssteigerung von Quantencomputern» dar. Sowohl für die Korrektur als auch für die Vermeidung von Fehlern gibt es keine umfassende Lösung. Noch wurde kein Weg gefunden, wie man eine fehlerfreie Quanten-Hardware herstellen könnte, und zur Implementierung einer Korrektur-Software oder eines Korrektur-Algorithmus sind Quantencomputer mit 50 bis 100 Qubits zu klein.

Bis zu einem gewissen Grad muss man damit leben, dass Fehler beim Quantenrechnen im Prinzip unvermeidlich sind, weil sich die Quantenzustände, die den konkreten Rechenschritten zugrunde liegen, nur mit Wahrscheinlichkeiten unterscheiden und beziffern lassen. Was sich hingegen erreichen lässt, sind Verfahren, die das Ausmass des Rauschens und der Störeinflüsse soweit begrenzen, dass die Berechnungen trotzdem zuverlässige Ergebnisse liefern. Informatiker bezeichnen ein zuverlässig funktionierendes Rechenverfahren als «robust» und sprechen in diesem Zusammenhang auch von der erforderlichen «Fehlertoleranz».

Genau das hat die Forschungsgruppe von Ce Zhang, ETH-Informatikprofessor und Mitglied des ETH AI Centers, nun vor kurzem erforscht – gewissermassen «zufällig» während der Arbeit über die Robustheit klassischer Wahrscheinlichkeitsverteilungen und um bessere Systeme und Plattformen für maschinelles Lernen zu bauen. Zusammen mit Nana Liu, Professorin der Shanghai Jiao Tong Universität und mit Bo Li von der Universität von Illinois in Urbana-Champaign, hat sie einen neuen Ansatz entwickelt, mit dem sie für bestimmte Quantenmodelle des maschinellen Lernens nachweislich die Robustheitsbedingungen angeben kann, unter denen gewährleistet ist, dass die Berechnung eines Quantencomputers zuverlässig erfolgt und das Ergebnis korrekt ist. Ihren Ansatz, der zu den ersten seiner Art zählt, haben die Forschenden in der Wissenschaftszeitschrift «npj Quantum Information» veröffentlicht.

Gewappnet gegen Fehler und Hacker

«Als wir feststellten, dass die Quantenalgorithmen so wie die klassischen Algorithmen anfällig sind auf Fehler und Störungen, haben wir uns gefragt, wie wir diese Fehlerquellen und Störeinflüsse für bestimmte Aufgaben des maschinellen Lernens abschätzen sowie die Robustheit und die Zuverlässigkeit des gewählten Verfahrens gewährleisten können», sagt Zhikuan Zhao, Postdoktorand in Ce Zhangs Gruppe, «Wenn wir das wissen, können wir den Rechenergebnissen vertrauen, selbst wenn sie verrauscht sind.»

Diese Frage haben die Forschenden am Beispiel der Quantenklassifizierungsalgorithmen untersucht – schliesslich sind Fehler bei Klassifizierungsaufgaben heikel, da sie sich auf die reale Welt auswirken können, zum Beispiel wenn giftige Pilze als ungiftig klassifiziert würden. Vielleicht am wichtigsten ist, dass die ETH-Forschenden – inspiriert von früheren Arbeiten anderer Forschenden bei der Anwendung von Hypothesentests im klassischen Bereich – mit der Theorie des Quantenhypothesentestens, mit der sich Quantenzustände unterscheiden lassen, einen Schwellenwert ermittelten, ab dem die Zuordnungen des Quantenklassifikationsalgorithmus garantiert korrekt und seine Voraussagen robust sind.

Mit ihrem Robustheits-Verfahren können die Forschenden sogar feststellen, ob die Klassifizierung eines fehlerhaften, verrauschten Inputs dasselbe Ergebnis liefert wie ein sauberer Input. Aus ihren Erkenntnissen haben die Forschenden auch ein Schutzkonzept entwickelt, mit dem sich die Fehlertoleranz eines Berechnungsvorgangs angeben lässt, und zwar unabhängig davon, ob ein Fehler eine natürliche Ursache hat oder durch Manipulation bei einem Hackerangriff entstanden ist. Ihr Robustheitskonzept funktioniert bei Hackerangriffen und bei natürlichen Fehlern.

«Das Verfahren lässt sich auch auf eine breitere Klasse von Quantenalgorithmen anwenden», sagt Maurice Weber, Doktorand bei Ce Zhang und Erstautor der Publikation. Da der Einfluss von Fehlern beim Quantenrechnen mit der Grösse des Systems zunimmt, forschen er und Zhao nun an diesem Problem. «Wir sind optimistisch, dass sich unsere Robustheitsbedingungen als nützlich erweisen, zum Beispiel in Verbindung mit Quantenalgorithmen, die dafür entwickelt wurden, um die elektronische Struktur von Molekülen besser zu verstehen».