Das Geheimnis einer guten Lösung
Der Mathematiker Siddhartha Mishra gewinnt den diesjährigen Rössler-Preis für seine Forschung über Lösungen für hochkomplexe Strömungs- und Wellenphänomene. Gewürdigt wird er für seine Beiträge zu schnelleren und präziseren Vorhersagen zu Wetter, Klima und Tsunamis und zu den Computersimulationen, die sie ermöglichen.

Ursprünglich hatte Siddhartha Mishra Physik studieren wollen. In seiner Kindheit in Bhubaneswar, der Hauptstadt des indischen Bundesstaats Odisha, träumte er davon, zu erfahren, «was die Sterne zum Scheinen bringt». Im Studium realisierte er, dass ihm der mathematische Zugang zur Welt mehr lag als der experimentelle, und so schloss er in der Mathematik ab. Die Hinwendung zur wirklichen Welt und zu physikalischen Erscheinungen hat sich ihm bis heute erhalten. Zu den Themen, die er als Mathematiker untersucht, zählen typischerweise dynamische Strömungen, Flüssigkeiten oder Gase (Fluide), die zum Beispiel bei Wetter, Klima oder Lawinen eine Rolle spielen, sowie wellenartige Phänomene, wie sie bei Tsunamis oder explodierenden Supernovas auftreten.

Wenn ein Mathematiker wie Mishra ein Phänomen der Natur ergründet oder eine technische Fragestellung in Angriff nimmt, dann betrachtet er sie zunächst einmal als ein System. All diese Systeme, ihr Verhalten, ihre Entwicklung und ihre Veränderungen lassen sich mathematisch in der Form bestimmter Gleichungen beschreiben. Die Gleichungen, die sich besonders eignen für Vorgänge, die an Bewegung und Veränderung gekoppelt sind, heissen seit ihrer Erfindung durch Isaac Newton (1642-1726) und Gottfried Wilhelm Leibniz (1646-1716) Differentialgleichungen. Sie sind zentral für Siddhartha Mishras Forschung.
Brücken schlagen für chaotische Strömungen
Zwei seiner aussergewöhnlichsten Durchbrüche hat Mishra bei den sogenannten Euler-Gleichungen erzielt: diese Gleichungen sind nach dem Schweizer Mathematiker Leonhard Euler (1707-1783) benannt. Er entwarf eine wichtige Klasse partieller Differentialgleichungen, die Strömungen beschreibt, wie sie zum Beispiel um einen Tragflügel herum entstehen. Mishra löste eine Frage der Euler-Gleichungen, die 30 Jahre lang offen war, indem er einen neuen Algorithmus für ein Näherungsverfahren vorschlug. Ausserdem entwickelte er einen Lösungsansatz für bestimmte Euler-Gleichungen, mit dem sich die Dynamik instabiler, chaotischer und turbulenter Strömungen genauer bestimmen lässt.
Für seine Forschung auf dem Gebiet der nichtlinearen partiellen Differentialgleichungen hat Siddhartha Mishra den Rössler-Preis 2023 erhalten. Ausserdem würdigt der höchstdotierte Forschungspreis der ETH Zürich, dass Mishra eine Brücke schlägt zwischen den mathematischen Grundlagen und ihrer Anwendung in Forschung und Industrie. So hat er beispielsweise robuste, effiziente Algorithmen entworfen, mit denen sich nichtlineare partielle Differentialgleichungen schneller und genauer auf Supercomputern simulieren lassen. Diese Simulationen eröffnen neue Wege zur Lösung realer Probleme in Forschungsgebieten wie der Astrophysik, Sonnenphysik, Geophysik, Klimadynamik und der Biologie.
Abstrakte Gleichungen für reale Probleme
Reale Probleme sind das A und O von Siddhartha Mishras Forschung: «Die Phänomene, mit denen ich mich beschäftige, haben eine reale Auswirkung auf die Welt», sagt Mishra, «und die Auswirkungen von Veränderungen zu verstehen, ist der Schlüssel, um physikalische und technische Prozesse in der realen Welt zu begreifen.» Für seine Forschung typische Fragen sind zum Beispiel: «Wie sehr verringert sich der Luftwiderstand, wenn an einem Flugzeug die Form des Flügels in einer bestimmten Weise verändert wird? Und wieviel Kohlenstoffemissionen lassen sich durch eine aerodynamischere Form einsparen?» Kennzeichnend für Mishra ist seine Anwendungsorientierung. Regelmässig arbeitet er mit Ingenieurforschenden und der Industrie zusammen. Zum Beispiel hat er mit Forschenden der Empa schnelle Algorithmen entwickelt, um ein additives, industrielles Fertigungsverfahren für den 3D-Druck zu simulieren. Dabei wird mit Mishras Algorithmen ein Laserstrahl in Echtzeit so positioniert, dass er die gewünschte Form aus einen Metallblock fräst.
«Das Erstaunliche an der Mathematik ist, wie ihre abstrakten Gleichungen immer wieder neue Lösungen und hochrelevante Anwendungen für Wirtschaft und Gesellschaft ermöglichen», sagt Max Rössler, der Stifter des Rössler-Preises, der selbst Mathematik an der ETH Zürich studierte, über Bahnberechnungen in der Raumfahrt promovierte und am Institut für Operations Research unterrichtete. «Die Forschung von Siddhartha Mishra belegt die unglaubliche Anwendbarkeit der Mathematik eindrücklich, indem seine Gleichungen zum Beispiel Vorhersagen zu Wetter, Erdbeben oder Tsunamis unterstützen oder auch produktive Anwendungen ermöglichen wie das 3D-Drucken mit Metallen in der industriellen Fertigung.»
Annäherungen an komplexe Verhältnisse
In der Regel beziehen sich die nichtlinearen partiellen Differentialgleichungen, die Mishra untersucht, auf reale Phänomene, die – wie Wolken, Tornados oder Sonnenstürme – sehr komplex und vielschichtig sind und viele Abhängigkeiten, Wechselwirkungen und Ungewissheiten enthalten. Diese Probleme sind oft so komplex, dass sie sich mit einfachen Gleichungen nicht vollständig beschreiben lassen. Eine Lösung erfüllt dann eine Gleichung, wenn sie beim Einsetzen konkreter Werte eine wahre, mit den gemessenen Tatsachen übereinstimmende Aussage erzeugt.

«In gewisser Weise ist alle Mathematik eine Annäherung.»Siddhartha Mishra
Bei hochkomplexen, multidimensionalen Naturereignissen arbeitet ein Mathematiker wie Mishra mit Annäherungen an die Lösungen der Gleichungen. Die Probleme aus der realen Welt lassen sich oft gar nicht ohne Näherungsverfahren lösen. «Die Natur selbst und die Gleichungen, mit denen wir die Natur modellieren, sind sehr oft zu komplex, um letztlich etwas anderes als Annäherungen zu erlauben», sagt Mishra, «in gewisser Weise ist alle Mathematik eine Annäherung, wie die antiken Griechen und die indischen Mathematiker im ersten Jahrhundert schon sagten.»
Heute stehen Mathematiker:innen wie Mishra leistungsstarke Computer zur Seite. «Supercomputer können die Differentialgleichungen für komplexe Systeme näherungsweise lösen», sagt Mishra. Den Rössler-Preis erhält Mishra auch dafür, dass er die «schwächeren» Näherungslösungen sehr sorgfältig formuliert und sie in Algorithmen überträgt. Die Qualität seiner Algorithmen besteht darin, dass sie die Struktur einer mathematischen Gleichung besonders gut bewahren und auf diese Weise die Genauigkeit der Simulationen erhöhen. Numerische Näherungsverfahren haben jedoch für Mishra nicht nur einen praktischen Nutzen, sondern sie spielen auch eine fundamentale Rolle, um die Gültigkeit, den Anwendungsbereich und die Wirkung einer Gleichung zu beweisen.
Maschinelles Lernen für Tempo und Genauigkeit
In jüngster Zeit hat Siddhartha Mishra, der Mitglied des ETH AI Centers ist, begonnen, sehr leistungsfähige Algorithmen des maschinellen Lernens zu entwerfen. Zunächst ging es ihm darum, die Rechenzeit der Simulationen zu verkürzen. Nun kommen vermehrt Fragen auf, wie maschinelles Lernen die Genauigkeit einer Simulation erhöhen und bisher unlösbare Probleme lösen könnte.
Für die Beschleunigung der Rechenzeit mithilfe maschinellen Lernens kann Mishra schon einige Beispiele vorweisen:
- Im Falle des 3D-Druckverfahrens für Metalle reduzierte sein Ansatz die Rechenzeit der Simulation von rund vier Stunden auf eine Zehntelsekunde (0,1 s).
- Bei einem Tsunami-Frühwarnsystem beträgt die Rechenzeit mit Mishras Lernansatz rund eine Hundertstelsekunde (10-2s). Zuvor dauerte es rund eine Stunde, um vom Erdbebenereignis an vorherzusagen, wie sich ein Tsunami entwickelt und ausbreitet.
-
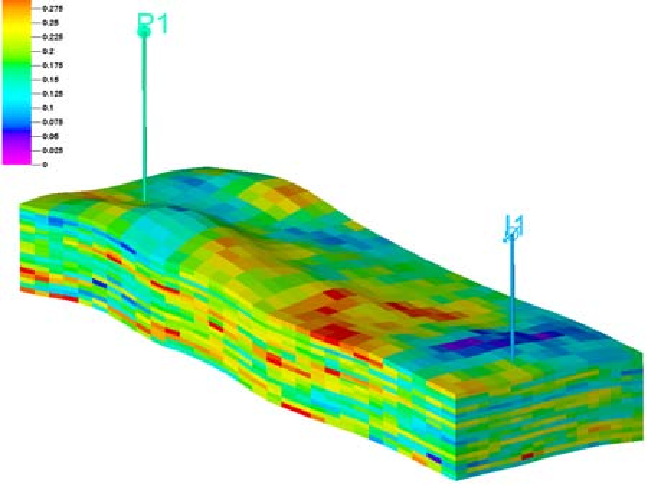
Das regenbogenfarbene Bild stellt eine Simulation der Ölkonzentration in einem Erdölreservoir dar. (Bild: ETH Zürich) -

Mishras persönlicher Favorit ist eine Stratocumulus-Wolkensimulation, die sehr schwierig zu berechnen war. (Bild: ETH Zürich) -
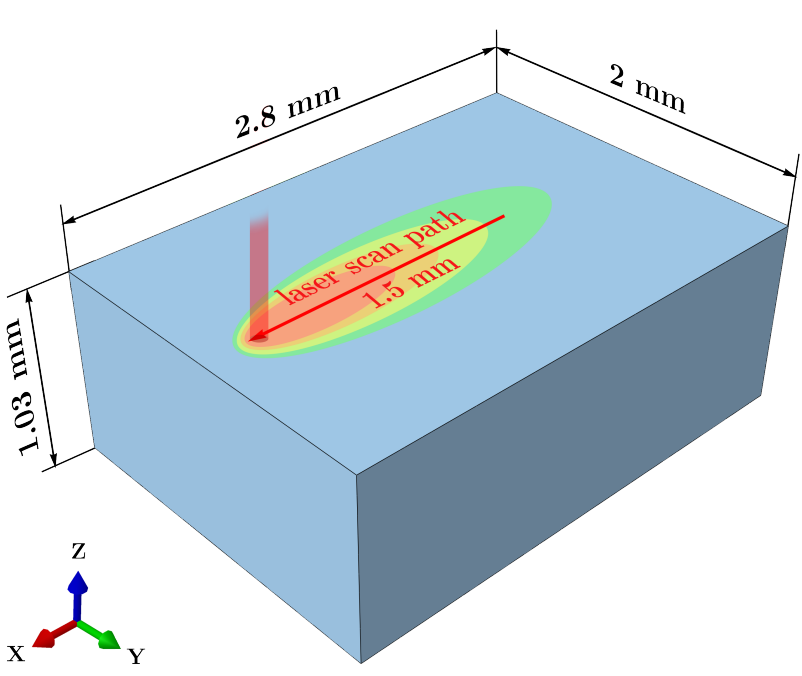
Zusammen mit Empa-Forschenden hat Mishra ein neues 3D-Druckverfahren für Metalle entwickelt. (Bild: ETH Zürich, Empa)
«Die Simulationen mit maschinellem Lernen sollen nicht nur zehnmal schneller sein, sondern zehntausend bis hunderttausendmal», sagt Mishra. Ein Beispiel, wie Lernalgorithmen die Genauigkeit einer Simulation erhöhen, kommt aus der geophysikalischen Forschung. Zusammen mit Yunan Yang, die zuletzt am Institut für Theoretische Studien forschte, und anderen Mitarbeitenden schlug er einen neuen Algorithmus für maschinelles Lernen vor, um geophysikalische Eigenschaften unter der Oberfläche durch seismische Bildgebung zu ermitteln, d. h. durch Aussenden seismischer Wellen in den Boden und Aufzeichnen ihrer Rückstrahlung in den Messstationen an der Oberfläche. Mishras und Yangs Algorithmen sind vier bis fünfmal schneller als bisherige Algorithmen, und sie sind auch zwei bis viermal genauer.

Auch für seine maschinellen Lernalgorithmen dient Mishra die Physik als Inspiration: zum einen verwendet er maschinelles Lernen für Fragen der Physik. Zum anderen nutzt er physikalische Prinzipien und Begriffe, um leistungsfähigere, robustere und zuverlässigere maschinelle Lernsysteme zu entwickeln – zum Beispiel, um die Bildgebung in der Neurologie zu schärfen.
Der Rössler Preis
Max Rössler vermachte 2008 der ETH Zürich Foundation zehn Millionen Franken. Mit dem Zins aus diesem Vermögen stiftet er einen jährlichen Förderpreis für ETH-Professor:innen in der Expansionsphase ihrer Forschungskarriere. Der Preis ist mit 200‘000 Franken die höchstdotierte Auszeichnung für Forschung an der ETH Zürich und wird jeweils am «Thanks Giving»-Anlass der externe Seite ETH Zürich Foundation verliehen. Der Preisstifter studierte an der ETH Zürich Mathematik und doktorierte über Bahnberechnungen in der Raumfahrt. Nach einem Forschungsaufenthalt an der Harvard University kehrte er an die ETH zurück und war von 1967 bis 1978 Senior Scientist und Lehrbeauftragter am Institut für Operations-Research. Später war er in der Vermögensverwaltung tätig, ehe er sich aus dem Geschäftsleben zurückzog. 2013 verlieh ihm die ETH Zürich den Titel eines Ehrenrats.
Weitere Informationen zum externe Seite Rössler-Preis.

Literaturhinweise
Bartolucci, F, de Bézenac, E, Raonić, B, Molinaro, R, Mishra, S, Alaifari, R. Are Neural Operators Really Neural Operators? Frame Theory Meets Operator Learning. arXiv:2305.19913v1 [cs.LG]. (2023). externe Seite 10.48550/arXiv.2305.19913
Molinaro R, Yang Y, Engquist, Mishra, S. Neural Inverse Operators for Solving PDE Inverse Problems. ETH Zurich Research Collection (2023). https://www.research-collection.ethz.ch/handle/20.500.11850/596104
Hosseini, E, Ghanbari, PG, Müller, O, Molinaro, R, Mishra, S., Physics Informed Neural Networks for Thermal Analysis of Laser Powder Bed Fusion Process. 2022. Available at SSRN: externe Seite https://ssrn.com/abstract=4189609 or doi: externe Seite 10.2139/ssrn.4189609
Kommentare
Noch keine Kommentare